Diffusion探究——DPMSolver采样器

0x0 写在前面#

DPMSolvers 由于其极高的效率成为了不少 diffusion based models 默认选用的采样器，本文将对 DPMSolver 、DPMSolver++ 、DPMSolvers Inversion 做出讨论。

参考的三篇论文如下：

阅读这些文章需要对 ODE 求解中的线性多步方法（包括欧拉方法）有了解，另外，需要对 Diffusion SDE 和 DDIM 中的概率流 ODE 有比较完备的理解。

0x1 热身#

我们有：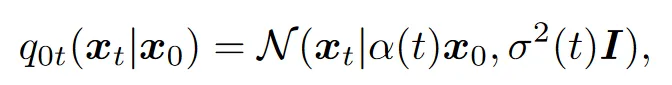

首先回顾宋飏博士的 Diffusion SDE：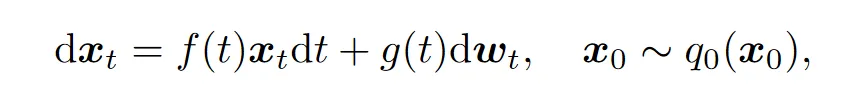

其中：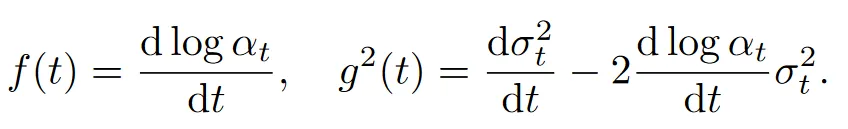

它的反向过程（去噪过程）为：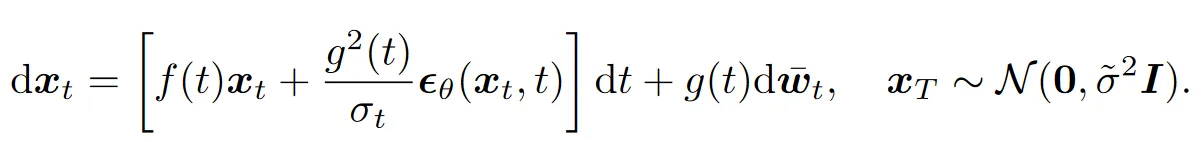

接下来是 DDIM 中提到的概率流 ODE ：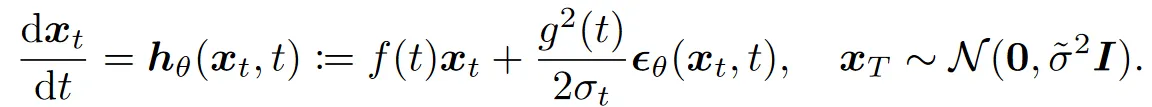

将不确定的布朗运动去掉了，使扩散过程变为确定过程，我们从而可以实现采样跳步和反演。

0x2 DPMSolver#

目标#

加速采样。

ODE精确解的探求#

作者路橙博士发现概率流 ODE 可以分为两个部分，其中 $f(t)x_{t}$ 是线性项， $\frac{g^{2}(t)}{2\sigma_{t}}\epsilon_{\theta}(x_{t}, t)$ 由于涉及到黑盒的神经网络模型，则是非线性的，所以概率流 ODE 是一种半线性 ODE 。在之前的工作中，大家将整个 ODE 当作黑盒来求解，使得线性部分和非线性部分都产生了误差。

对于形似概率流 ODE 的方程，我们在大一的数学分析课程中就学到过一种解析解法，即：

那么 ODE 的解可以写作：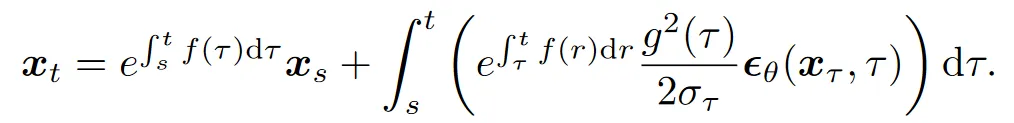

解的线性项可以精确求解，接下来讨论非线性项。

注意到，引入一个新的参数 $\lambda_{t}=log(\alpha_{t}/\sigma_{t})$ ，即对数信噪比的一半，可以极大地简化积分部分：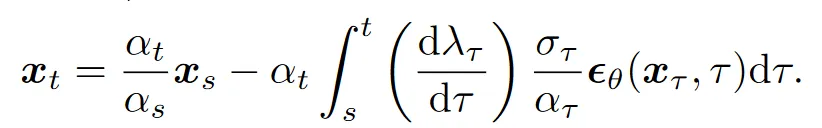

顺便完成了线性项的积分。到这里可以注意到， $\lambda$ 是关于 $t$ 的单调递减函数，所以可以直接换元，写成如下的形式：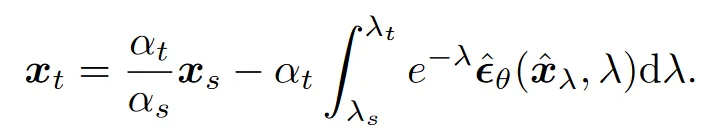

非线性项被转化为指数加权积分的形式，而这种形式的 ODE 已经被数学家们研究过了，并且有了形式化的解，参考其解法，我们研究以下方程的解：

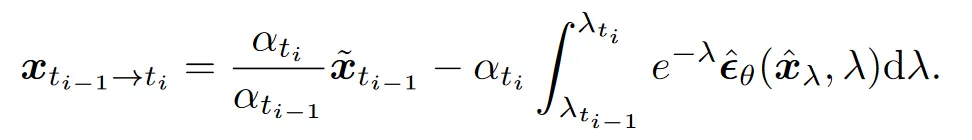
将关于 $\lambda$ 的神经网络函数在 $\lambd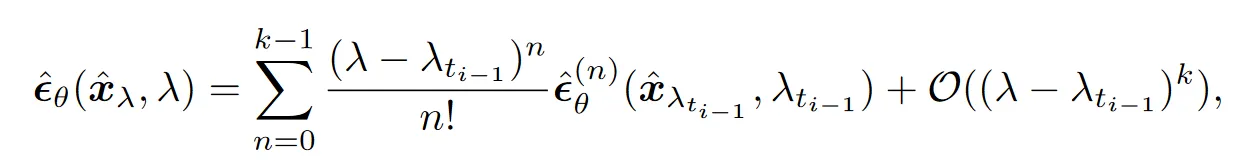a_{t_{i-1}}$ 处泰勒展开：

于是积分式变为：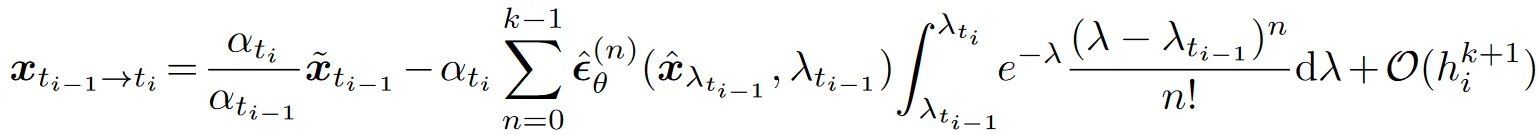

现在积分部分可以通过不断应用分部积分法来进行精确计算了，参考 Exponential Rosenbrock methods 或者论文附录即可。

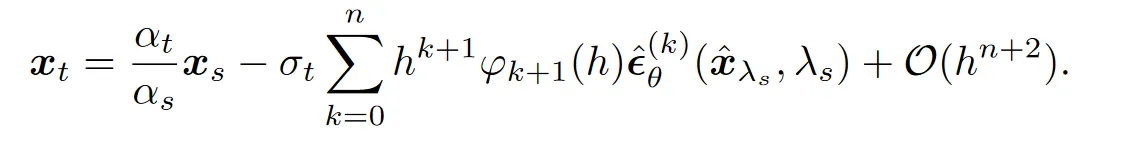
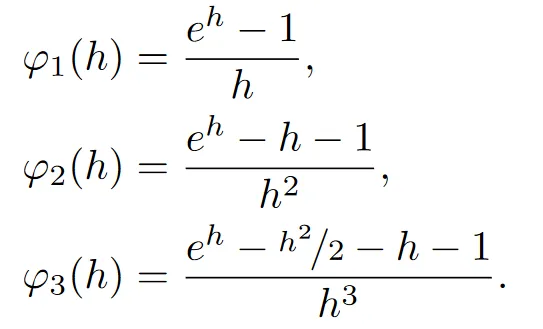
这样我们就可以尝试开始构造单步误差为 $O(h_{i}^{k+1})$ 的 $k$ 阶 DPMSolver 采样方法了。

采样方法构造#

当 $k=1$ 时，DPMSolver 的形式非常简单：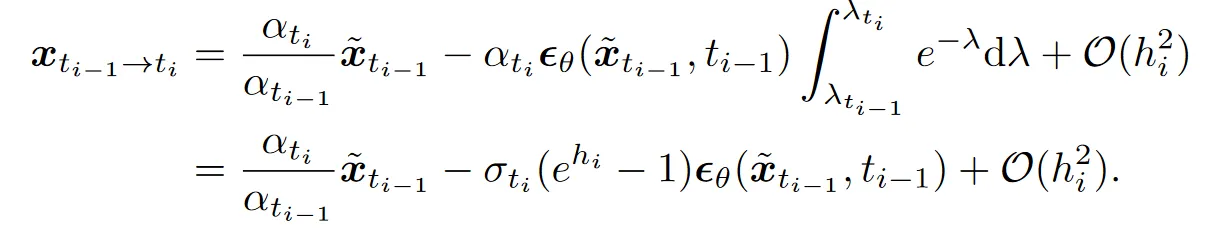

完全和上面的解析形式相同，也完全和 DDIM 相同。一阶收敛性很显然，把它扩展到全去噪过程，得到证明如下：

即对于全去噪过程，k 阶求解器的误差应该为 $O(h^{k})$ ，而对应的单步去噪，误差需要被控制为 $O(h^{k+1})$ 。下面的证明也是这样推导的，但不再重复这一步证明了。

当 $k=2,3$ 时，算法被写作：

两则算法都利用了中间量。如果是正常看到这里，又像笔者一样数理基础不扎实的话，可能就会一头雾水，下面分析一下这两则算法，首先，DPMSolver-2 在第 5 行跳步了，更便于理解的是附录中的算法 4 ：

这里的第 5 行经过化简即可得到上面的结果。另外还有一个问题在于，DPMSolver-2 的设计与前面的解析分析是不符的，这点也是在附录中写明的：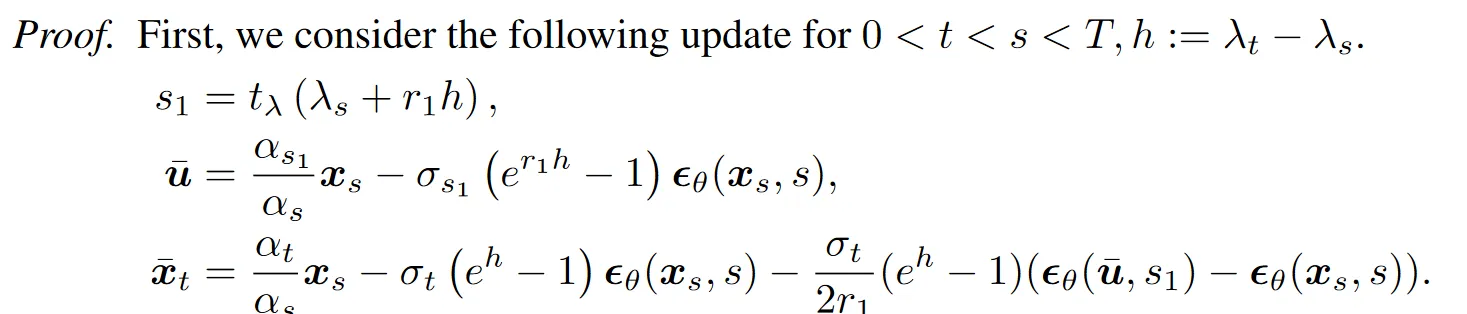

对于 $\bar{x}_{t}$ 的表达式，其第二项是正常的一阶量，第三项先根据中间量估计了 $\epsilon_\theta$ 的一阶导数，然后再将其代入作为二阶项，如果按照正常流程，结果应该是：

\frac{\sigma_{t}}{r}\left(\frac{e^{h}-1}{h}-1\right)(\epsilon_\theta(\bar{u},s_{1})-\epsilon_\theta(x_{s},s))

但没有这样设计，这是因为 $\bar{u}$ 并不是 $x_{s_{1}}$ ，而是它的一阶估计，如果按这样推下去，误差是 $O(h^{2})$ ，不满足二阶求解器的条件。还需要对它进行改写，拆为两部分，第一部分可由莱布尼兹性（假设）证明是收敛的，第二部分则可以通过 $h=0$ 处的泰勒展开证明，具体的证明如下：

故原式中第三项系数了构造是为了满足收敛条件。

DPMSolver-3 也是同理，这里不再赘述了。

实际应用#

自适应步长调度#

对于不同的 NFE（number of function evaluations）采取自适应的采样方法，即尽量使用高阶（比如 3 阶）的 DPMSolver ，当 NFE 无法被 3 整除时，则采用 2 阶或 1 阶进行估计。

离散时间采样#

论文前面的讨论都是针对连续时间 DPM 进行的，对于离散时间，只需要把离散时间步 $t$ 映射到对应的连续时间步 $\frac{t}{T}$ 即可。

与其他采样方法的比较#

DDIM#

DPMSolver-1 即为 DDIM ，DDIM 过程可以视为欧拉方法，但是它与其他形式（考虑其他自变量）的欧拉方法有所不同，DPMSolver 反向证明了 DDIM 的成功是因为它恰好利用到了概率流 ODE 的线性部分。

RK方法#

其他的用于对时间 t 求解 ODE 的线性多步方法会因为步长的不均匀变化而出现较大误差，但 DPMSolver 并没有这样的问题。

0x3 DPMSolver++#

目标#

解决高阶 ODE 求解器在 guidance scale 比较大时生图质量差的问题。

简单来说 guidance scale 的增大会放大模型的输出和导数，高阶求解器对此表现得更加敏感，如果超出收敛半径，就会出现上述情况。同时，guidance scale 的提高引起的输出放大也会直接导致生图质量变差，表现为图像饱和度过高等（train-test mismatch）。

不收敛原因分析#

ODE 的参数化不合理#

此前的高阶求解器都是针对噪声预测模型 $\epsilon_\theta$ 进行设计的，这对解的收敛可能有不利影响。

新的ODE及其精确解#

本文将针对数据预测模型 $x_{\theta}$ 设计高阶求解器。

噪声预测模型 $\epsilon_\t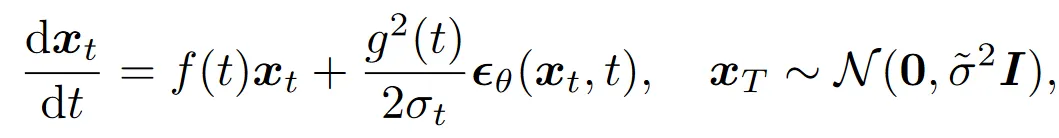heta$ 形式的 ODE 如下：

数据预测模型 $x_{\theta}$ 形式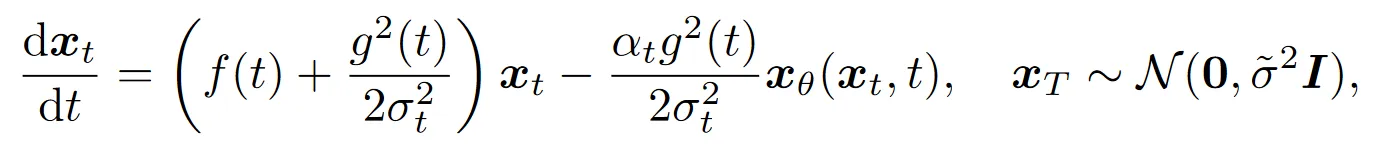的 ODE 如下：

其推导利用如下的等价关系：

x_{\theta}(x_{t}, t) = \frac{x_{t}-\sigma_{t}\epsilon_{\theta}(x_{t},t)}{\alpha_{t}}

对应 DDIM 中预测 $x_{0}$ 的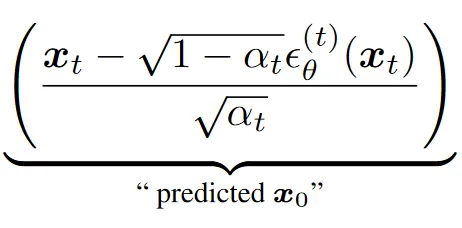部分：

这样的 ODE 设计更有利于解的收敛，而且也方便使用阈值方法来控制采样的边界，缓解 train-test mismatch。至于原因，会在后面讨论。

如法炮制 DPMSolver 的分析，可以得到新 ODE 的解的指数加权积分形式为：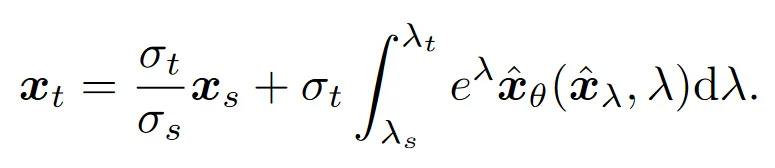

此解与原 ODE 的解是等价的，但是从数值解估计（即求解器设计）的角度来看，二者是不同的。

首先，两种解的线性项不同，其次，两种解的积分项不同。（原文就是这么说的）

同样对新解的积分项在 $\lambda_{t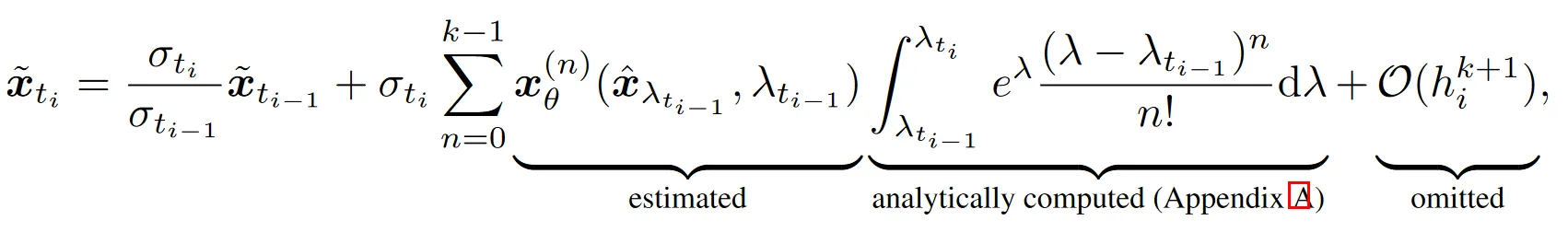_{i-1}}$ 处泰勒展开，得到：

作者这里说附录 A 里有对积分项的分部积分计算过程，但我并没有找到，不过与 DPMSolver 的解法推导只有一个系数不同。

采样方法构造#

一阶退化为DDIM#

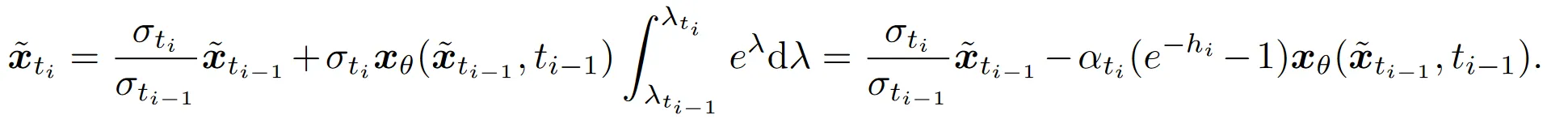
DPMSovler++(2S)#

2S 的 2 代表 2 阶，S 代表 Singlestep ，算法的流程与 DPMSolver-2 非常相似（尤其是把 $D_{i}$ 的结合顺序改变并在第 7 行展开后），基本只有参数不同。

展开后：

\alpha_{t_{i}}(e^{-h_{i}}-1)x_{\theta}(\tilde{x}_{t_{i-1}}, t_{i-1}) + \frac{\alpha_{t_{i}}}{2r_{i}}(e^{-h_{i}}-1)(x_{\theta}(u_{i}, s_{i})-x_{\theta}(\tilde{x}_{t_{i-1}}, t_{i-1}))

DPMSolver-2：

收敛性的证明也与之相似，虽然在本文的附录中写得更加形式化（吓人）了，实际上换汤不换药。

如前面所说，更高阶的版本与高 guidance scale 不适配，所以作者这里不再考虑 3 阶情况。

DPMSolver++(2M)#

这里的 M 代表 Multistep ，实际上可以视为一个小 trich ，如果按照 2S 版本来，需要考虑的时间步为 $\{t_{i}\}_{i=0}^{M}$ 以及 $\{s_{i}\}_{i=1}^{M}$ 总共 $2M+1$ 项，由于算法本身涉及到中间量，所以顺水推舟可以把每个 $t_{i}$ 都既当作目标量也当作求解下一个目标量的中间量，达到节约计算资源的效果。

用多步方法（参考 ODE 求解中的线性多步方法）来估计高阶导数是更精确的，除了上述提高性能的作用，2M 版本实际上也是更好的。这一点也被实验证明了。

相比 DPMSolver 提出的所谓自适应 NFE 的方法，2M 版本不再需要推理步数 $N$ 能整除总时间步 $M$ 了。

至于它的收敛性证明，也和 2S 版本非常相似，但并非完全相同，涉及到了多步间的误差传递。

阈值方法#

由于 DPMSolver++ 是针对 $x_{\theta}$ 设计的，所以阈值方法能直接与其结合起来使用，以提高生图质量。

SDE快速精确求解#

本文对 SDE 的求解也进行了研究。

再次回顾 Diffusion SDE：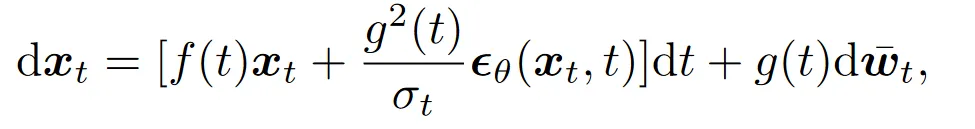

同样使用之前的 $\lambda$ 进行换元，对于反向时间维纳过程有：

dw_{\lambda}=\sqrt{-\frac{d\lambda_{t}}{dt}}d\bar{w}_{t}

对于 VP（方差保持，Variance Preserving，与之对应的是方差爆炸，VE）型扩散模型，有 $\alpha_{t}^{2}+\sigma_{t}^{2}=1$ ，利用这一条件可以得到 SDE 变元后仍然简洁的形式：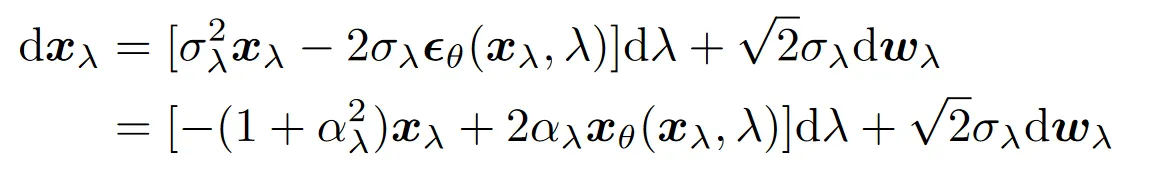

再次如法炮制，得到它的解：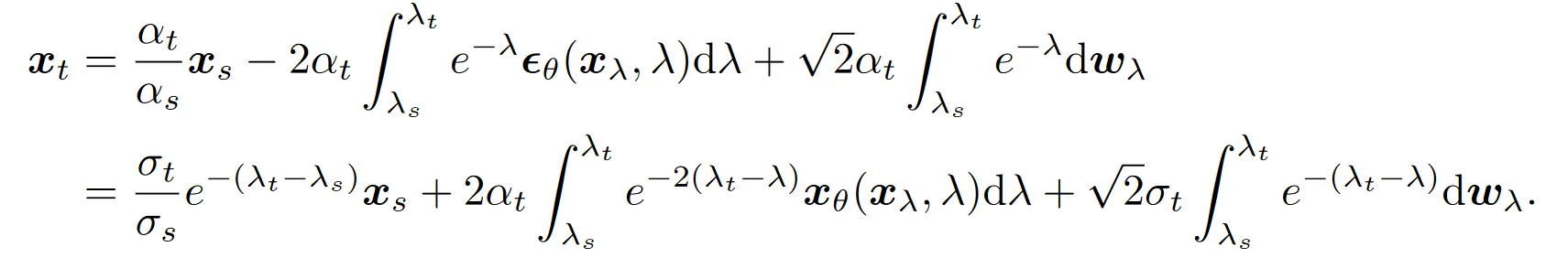

解的最后一项是伊藤积分：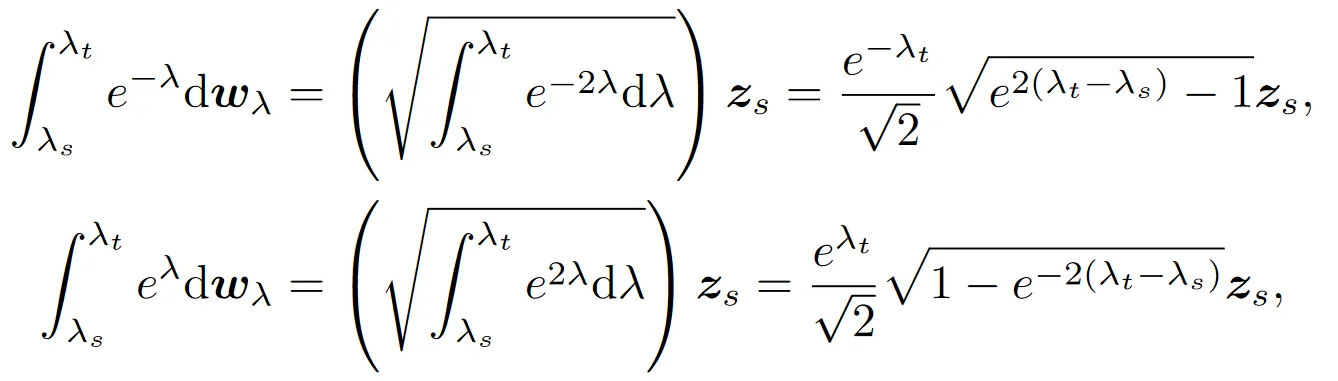

其中 $z_{s}$ 是标准高斯噪声。

至此，解决掉维纳过程（或者说布朗运动，又或者不确定噪声）项之后，剩下的部分我们又可以套用上面的分析，得到如下四个解的形式。

与其他采样方法的比较#

作为DDIM的高阶泛化形式#

首先，DPMSolver++ 也可以在一阶情形下退化为 DDIM ，其次，SDE-DPMSolver++ 也可以在一阶情形下退化为 DDIM 方差不为 0 的形式。

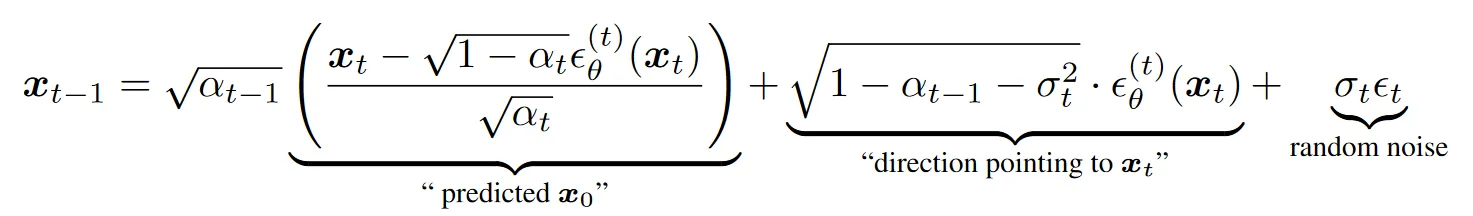
上述方差指的是上图中的方差 $\sigma_{t}$ ，本文将它表示为 $\eta$ ，那么事实上，SDE-DPMSolver++ 对应的就是 $\eta=\sigma_{t}\sqrt{1-e^{-2h}}$ 的情况。

相比上一代DPMSolver#

由于有等价关系：

x_{\theta}(x_{t}, t) = \frac{x_{t}-\sigma_{t}\epsilon_{\theta}(x_{t},t)}{\alpha_{t}}

我们可以将其带入后把 DPMSovler++ 的结果展开：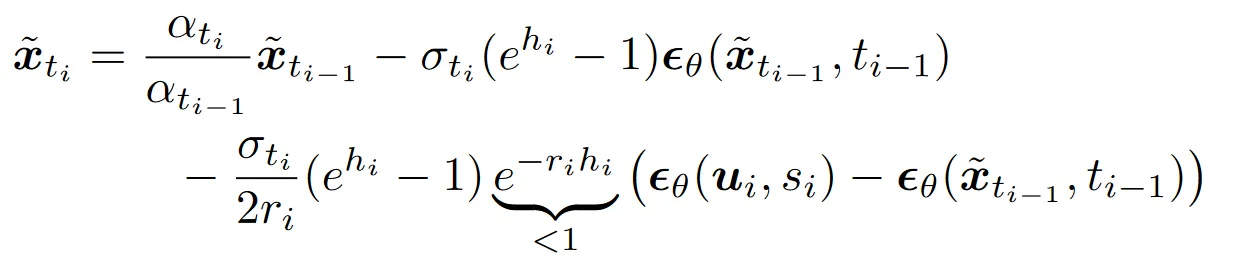

对应的 DPMSolver 的解是：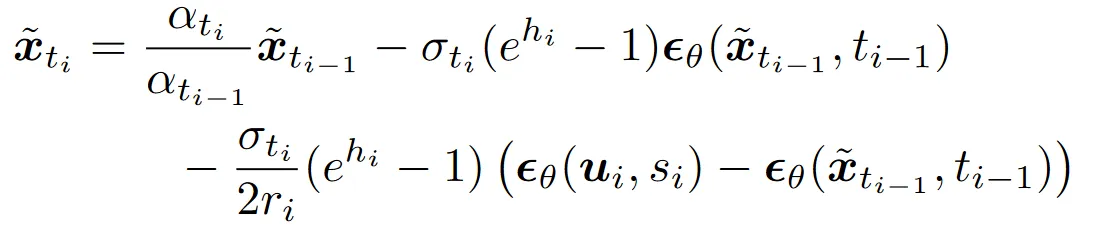

可以注意到它们之间仅仅相差一个系数 $e^{-r_{i}h_{i}}$ ，由于这个系数小于 1 ，作为一阶全导数的估计的系数，可以对导数的误差起到缩减作用，从而缓解本文提出的高阶求解器不适配高 guidance scale 的问题，也削减了正常求解的误差。

0x4 DPMSolvers Inversion#

反演#

由于 DDIM 带来了确定的去噪过程，我们可以把模型生成的图像反演回初始噪声，这为很多下游任务提供了便利，比如类似 Gaussian Shading、Tree-Ring 的扩散语义水印工作，和图像编辑等 AIGC 工作。

难点#

DPMSolvers 的高阶项在反演过程中难以精确获取
DPMSolvers 极大地扩大步长，使得一些基于估计的方法（比如 DDIM Inversion ，往往需要步长小）误差很大
DPMSolver++(2M) 中使用的多步方法需要参考未知的状态
反演在 guidance scale > 1 的情况表现不好
有些方法为了保证反演的精度，修改了去噪过程，这将导致根据标准方法采样出来图像无法被正常反演

前三点是 DPMSolvers Inversion 的困难，后面两点则是目前整个反演研究面临的困难。

DDIM的精确反演#

DDIM 是前向欧拉方法，Naive DDIM Inversion 如下：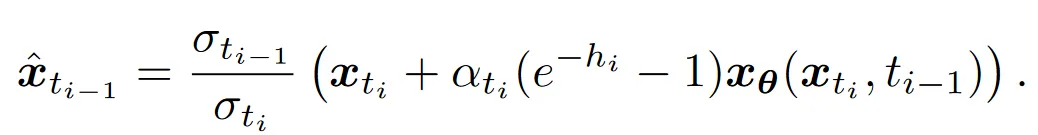

注意到最后用 $x_{\theta}(x_{t_{i}},t_{i-1})$ 来估计 $x_{\theta}(x_{t_{i-1}},t_{i-1})$ ，实际也是前向欧拉方法。

本文作者提出了一种后向欧拉方法：

有点故弄玄虚，实际是先根据 Naive DDIM Inversion 估计一个值 $z_{t}'$ ，然后用估计值重新去噪得到 $z_{t-1}'$ ，通过计算 $z_{t-1}'$ 与 $z_{t-1}$ 的 MSE 的梯度来优化 $z_{t}'$ ，直到收敛，谈不上高明的方法。

对于 VAE 的 Decoder Inverison，作者也采取了类似的方法：

DPMSolvers高阶项的精确反演#

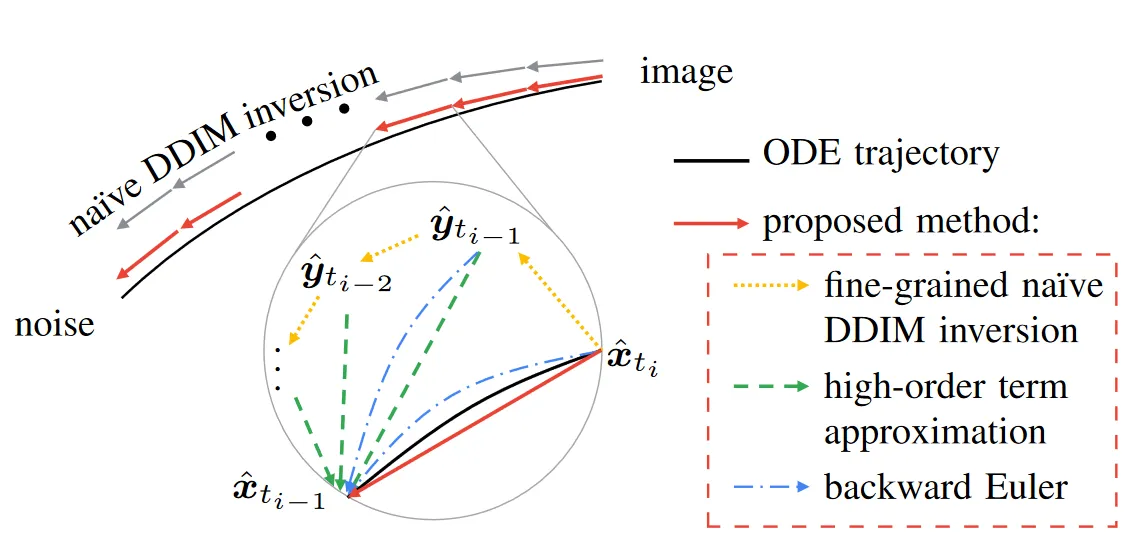
该算法看着吓人，实际上也是简单的优化过程。首先，作者认为高阶项对反演的影响是相对小的，所以可以直接用步长更小的 DDIM 来估计，如此得到高阶项之后，又可以用反向欧拉方法来进行优化了。

因为所谓反向欧拉方法的优化过程太鲁棒了，所以本文这种粗糙的高阶量估计也能起作用，它们地作用只是为优化过程确定一个还算不错的初值罢了。

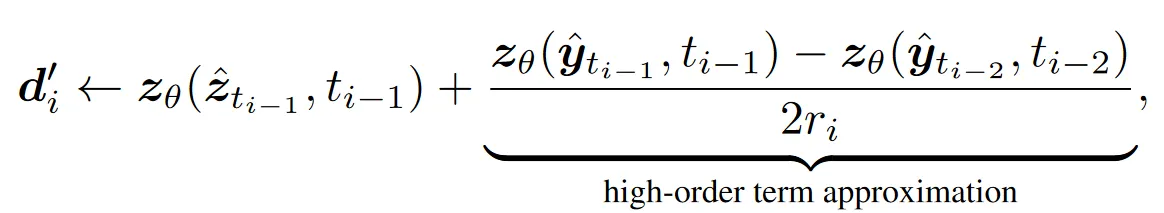
0x5 讨论#

评价#

路橙博士两篇 DPMSolvers 的工作很硬核，推导都比较严谨，在笔者读过的所有 AI-related 的文章中属于很硬的一档了，数学推导所用的知识倒都属于本科数学范畴，不难理解，但是需要较强的注意力去完成那一步关键的换元。同时 DPMSolver++ 中也坦诚地说明了 DPMSolver 等高阶求解器的问题，并给出了误差原因分析和解决方法，两篇文章的讨论中更是很好地总结了其他采样方法（比如 R-K 等纯线性多步方法）的一些缺陷。

至于最后的关于 DPMSolvers Inversion 的文章，它的背景介绍部分写得比较完备，对下游各种应用的实验也比较充分，但是就方法本身来说，并不精彩，甚至可以称作平凡，不知道是怎么投中 CVPR 2024 的，全文最硬的地方恐怕是对 FPI 方法的缺陷分析了。

思考#

关于线性多步方法#

DPMSolvers 的来历被写得非常精彩，但它的本质很简单，如果读者数学直觉够强（换元换回去）的话就会发现其构造出来的推导式其实就是经典的两步欧拉（Two-step Adams–Bashforth）：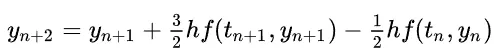

只需要对神经网络进行泰勒展开就可以推导出来，文章中的换元和指数权重积分可以看作是作者个人发现这种方法的思维路径，实际上的 DPMSolvers 是非常简单而优美的。至于 ++ 版本为什么和原版是不同的结果，其实也是因为它们对不同的网络函数进行了泰勒展开。

关于反演#

如果没有非常高的精度需求，完全可以用 Naive DDIM Inversion 。同期有一篇工作 GNRI(ICLR 2024) 做得更好，从结果来看，既快又好，不过似乎没有引起更大的关注，后面可能会就这篇工作和 BELM 以及其他同类文章进行一些比较。

0x6 引用#

@article{
  title   = "Diffusion探究——DPMSolver采样器",
  author  = "Jindong Yang",
  journal = "0xd009.github.io",
  year    = "2025",
  month   = "January",
  url     = "https://0xd009.github.io/posts/Diffusion探究——DPMSolver采样器/"
}